All’inizio degli anni ’80 il premio Nobel per la fisica Richard Feynman si pone la domanda se fosse stato possibile, attraverso un computer classico, simulare la meccanica quantistica. La risposta che lo stesso Feynmann si dà è che no, attraverso un computer classico non è possibile simulare la meccanica quantistica.
Infatti, sebbene sia possibile attraverso i computer classici , elaborare calcoli di meccanica quantistica e quindi emularne il comportamento non è possibile ricreare in un computer classico un comportamento analogo a quello della meccanica quantistica.
Da qua la necessità di iniziare la ricerca per sviluppare un computer quantistico.
Certo, dire che in un computer classico non è possibile emulare il comportamento della meccanica quantistica, può lasciare spiazzati e la domanda che sorge spontanea è: ma se si può emularne il comportamento perché non è possibile anche simularlo?
Per capire questo bisogna avere delle idee basilari sulla meccanica quantistica, in particolare poche e per niente intuitive regole che sembrano uscite dal cappello di un mago.
Le regole basilari
Sebbene la Fisica quantistica sia alla base dei computer quantistici, come la fisica classica è alla base dei computer classici, non è necessario conoscerla per poter capirne il principio di funzionamento e la stessa matematica (solo quella che è alla base dei computer quantistici non della fisica quantistica) non è particolarmente impegnativa.
Diciamo subito che (per quanto contro intuitivo possa sembrare) dobbiamo considerare la possibilità che un sistema fisico nella meccanica quantistica può trovarsi contemporaneamente in tutti gli stati possibili (sovrapposizione coerente di stati). Per semplificare il concetto possiamo dire che se un elettrone può passare da due fenditure, una a destra e una a sinistra, passerà contemporaneamente per entrambe.
In realtà il concetto è molto astratto e riuscire a darne una rappresentazione mentale avulsa dalla matematica che ne sta alla base è veramente difficile.
L’altro concetto da sapere è chiamato entanglement e consiste nella possibilità che due particelle che hanno precedentemente interagito in qualche modo, se separate e messe a distanze elevate, possono ancora interagire nello stesso istante: se modifico la prima la seconda subirà la stessa modifica istantaneamente.
Com’è possibile tutto questo? Per capirlo bisogna sapere che esiste un confine tra la fisica classica e la fisica quantistica, e questo confine prende il nome di lunghezza di Planck: al di sotto di questa misura tutte le regole della fisica classica non funzionano più ma si utilizza la “funzione d’onda” che è l’incognita dell’equazione di Schrödinger e che rappresenta l’ampiezza di probabilità di trovare la particella in un preciso istante; bisogna però considerare che, sebbene l’evoluzione della funzione d’onda è determinata dall’equazione di Schrödinger, il suo risultato è deterministico.
Finiamo con un esempio per confondere ancora di più le idee: se io considero un sistema composto da un’auto che si muove lungo una strada diritta con un’accelerazione costante potrò sapere in qualunque istante dove si trova ed a quale velocità; in meccanica quantistica, se misuro una particella che si muove in una determinata direzione, non potrò sapere, contemporaneamente, la posizione ed il momento.
Se si capiscono questi concetti che possono sembrare contro intuitivi capire il principio di funzionamento di un computer quantistico diventa abbastanza semplice.
I Qbit
Alla base dei computer quantistici ci sono i Qbit, che come i classici bit possono avere valore 1 e 0.
Mentre nei computer classici il bit corrisponde alla presenza o assenza di un segnale, non è così per i qbit che possono essere rappresentati come un vettore a due dimensioni di modulo (lunghezza) pari a 1.
I Qbit hanno due valori di base |0> e |1> (il simbolo | > è la notazione di Dirac ed indica uno stato quanto-meccanico); ogni valore può assumere lo stato di Ground:
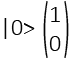
E lo stato eccitato
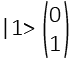
Ma, come abbiamo visto precedentemente, può trovarsi anche in una situazione di sovrapposizione e quindi essere in entrambi gli stati, in questo caso viene rappresentato dalla funzione:
|ψ> =α|o>+β|1>
Con α e β che rappresentano la possibilità che il nostro Qbit si trovi in un determinato stato altri qbit standard in sovrapposizione sono quindi:
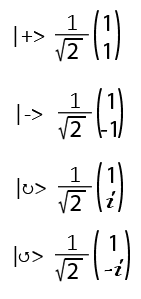
È importante sottolineare che |ψ> non rappresenta un’ulteriore stato come 0 e 1 altrimenti non sarebbe più un sistema binario ma ternario!
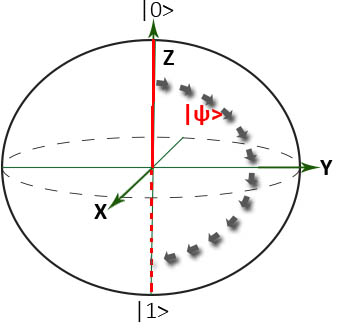
Dunque |ψ> alla fine è un vettore in uno spazio che però non è facilmente disegnabile o immaginare in quanto α e β sono numeri complessi. La rappresentazione più utilizzata è quella della sfera di Bloch che ci permette anche di fare chiarezza su quanto detto fino ad ora:
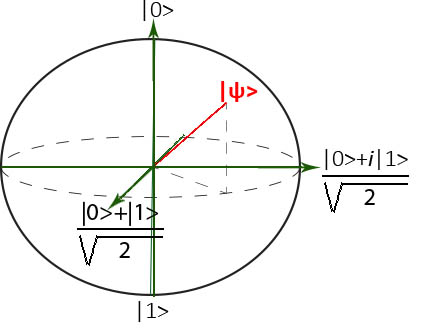
Nella sfera di Bloch abbiamo rappresentato il nostro vettore |ψ> in un punto qualsiasi della sfera che ha un angolo φ con l’asse X e θ con l’asse Z e, visto che la sfera ha infiniti punti, può – teoricamente- trovarsi in infinite posizioni
Per chi ha un po’ di dimestichezza con gli operatori logici classici possiamo immaginare che se un Qbit si trova nello stato |0> e applichiamo una rotazione lungo l’asse delle X cambia stato e diventa |1> e quindi questa operazione può essere considerata al pari di un NOT nella logica binaria classica.
Differenza tra computer classico e quantistico
Nei computer classici, abbiamo detto nell’introduzione, si utilizzano i bit che hanno valore 0 oppure 1. Da solo un bit vuol dire poco ed è per questo che vengono raggruppati insieme per trasformarsi in operazioni e prendono il nome di registri all’interno della CPU di un computer.
Quando, ad esempio di parla di processori a 64 bit ci si riferisce alla dimensione dei registri della CPU. All’inizio i registri erano costituiti da 8bit (che è ancora l’unità di misura del Byte). La capacità di immagazzinare ed elaborare l’informazione è 2 (il numero di stati disponibili in un bit) elevato al valore del registro. Quindi se si parla di 8bit ci si riferisce al valore di 255, se si parla di 16bit 65535, e così via. Se volessimo fare due conti vediamo che con gli attuali computer a 64 bit parliamo di un valore intorno a 18.446.744.073.709.551.615!
Tutte le operazioni che un computer può eseguire sono solo 7 che si combinano tra di loro e sono quelle della logica booleana (OR, NOT, AND, NAND, XOR, NOR, XNOR); quando un computer classico deve fare un’operazione lavora in maniera “simile” al nostro cervello: quando noi facciamo, ad esempio la somma 19+12 calcoliamo prima 9+2 (la somma delle unità) e riportiamo 1, poi ripetiamo l’operazione e sommiamo 1+1 (le decine) ed il valore riportato dall’operazione precedente utilizzando sempre le operazioni.
I computer funzionano grosso modo allo stesso modo, ripetendo l’operazione N volte in base a quanti bit sono implicati nell’operazione stessa. Quindi avrò una serie di passaggi alla fine di ognuno dei quali avrò uno stato definito dei miei registri fino a quando i bit non saranno esauriti; nel caso della somma di due o più valori, ad esempio un computer utilizzerà le operazioni OR per fare la somma e AND per il riporto.
Anche i computer quantistici utilizzano dei registri e, anche loro le operazioni che possono fare non sono moltissime ma, a differenza dei loro predecessori, grazie alla sovrapposizione di stati, dopo ogni passaggio il Qbit si troverà in tutte le possibili combinazioni contemporaneamente. I registri che contengo i Qbit, invece non saranno mai in tutte le combinazioni possibili ma solamente a 2n possibili combinazioni dove N è il numero di Qbit che compone il registro; inoltre può capitare che si voglia utilizzare un Qbit come Qbit di controllo e quindi le combinazioni saranno 2n-1 in quanto 1 Qbit mi darà sempre lo stesso risultato.
Un’altra differenza appare nel momento in cui si va a misurare il valore del registro del Qbit: non avrò più il valore 1 o il valore 0, ma grazie sempre alla sovrapposizione avrò una certa probabilità che risulti uno dei due valori, e questa probabilità è legata ai coefficienti α e β dell’equazione vista precedentemente, in particolare il |α|2 avrà una certa probabilità di avere come risultato |0> e il |β|2 di essere |1> .
Un’altra di particolarità dei Qbit è dovuta all’ entanglement: se prendo 2 Qbit che faccio “interagire” insieme creando uno stato, appunto, di entanglement, quando li separo, se il primo mi restituirà |1> quando misurato, anche il secondo (indipendentemente da quanto sia distante dal primo e dal suo stato) mi restituirà|1>, mentre se misurato separatamente mi potrà restituire, tranquillamente un altro risultato.
Le porte logiche dei computer quantistici poi si occupano di “manipolare” lo stato di sovrapposizione quantistica del Qbit e restituisce in output uno stato diverso di sovrapposizione quantistica “alterandone” le probabilità. Quando si misurerà il risultato tutte le possibilità collasseranno in uno stato di 0 o 1, ovvero il risultato con la relativa probabilità.
Ecco perché i computer quantistici processano tutte le combinazioni possibili in un unico processo e perché risultano più veloci dei computer normali. Non importa se la mia è solo una probabilità, se questa probabilità esce 10.000 volte vuol dire che può tranquillamente essere considerato il risultato esatto e chi pensa che questo sia un modo “lento” di operare perché la stessa operazione deve essere ripetuta più volte deve considerare che la velocità di elaborazione di un computer quantistico della stessa operazione è molto maggiore di quello di un computer classico per la stessa operazione ripetuta una sola volta. Le uniche volte nelle quali le operazioni non sono ripetute, ovviamente, sono nel caso che la probabilità sia del 100% ovvero il risultato sia|1>.
Fino ad ora abbiamo parlato di probabilità ma è importante avere in mente il concetto che quando si parla di probabilità nei computer quantistici ci si riferisce ad un’ampiezza di probabilità esprimibile tramite la campana gaussiana e non dobbiamo confonderci con la casualità di un risultato.
A chi serve un computer quantistico?
Per far funzionare un computer si utilizzano quelli che vengono chiamati algoritmi, ovvero una serie di istruzioni che eseguono una serie di operazioni per arrivare ad un risultato, e poco importa che si utilizzi la programmazione strutturata o ad oggetti, il concetto di algoritmo non cambia: sempre operazioni ed istruzioni serializzate sono.
Nei computer quantistici, invece abbiamo appena visto, le operazioni tendono ad essere elaborate in parallelo ed è lì che la maggior velocità di elaborazione entra in gioco.
Risulta quindi evidente che utilizzare un computer quantistico per vedere un film in full HD, navigare in internet, progettare un grattacielo o qualsiasi altro tipo di programma classico non ha molto senso, anzi potrebbe risultare più lento nell’elaborazione di un computer classico. Dove invece l’elaborazione quantistica, dà il massimo di sé, è (oltre che per i problemi di fisica quantistica) appunto nelle operazioni che devono essere parallelizzate e per le quali gli algoritmi devono essere scritti appositamente.
Gli esempi dove l’utilizzo di un computer quantistico e che più colpiscono l’immaginazione sono la fattorizzazione dei numeri primi, della decrittazione dei codici segreti come quelli che stanno alla base della RSA, e l’analisi dei Big Data.
Non stupisce quindi che tra i maggiori investitori nella ricerca sui computer quantistici, e tra i primi ad aver creato un vero computer quantistico funzionante, vi sia Google, leader nel trattamento di dati tramite i suoi servizi di ricerca nel web e di cloud.
Anche IBM ha sviluppato un suo computer quantistico e, a differenza di Big G, ha rilasciato anche parecchie specifiche, dando la possibilità a chiunque, tramite un servizio di cloud, di provare a programmare il proprio computer quantistico.
Quale futuro?
Indubbiamente il futuro è anche dei computer quantistici che però non sono un sostituto dei classici computer e non lo saranno ancora per parecchio tempo.
Questo però non esclude che negli ultimi anni l’interesse per i computer quantistici è notevolmente aumentata; Microsoft, ad esempio, ha mostrato il suo interesse per la programmazione dei quantum computer rilasciando Q# per il frameworks .Net che permette di creare programmi per i computer quantistici, mentre il fatto che ancora non esista uno standard, lascia aperto un buco che sarà riempito da chi riuscirà ad imporsi per primo come leader (come è accaduto per il computer PC IBM a metà degli anni ’80 del secolo scorso).
Le dimensioni e le peculiarità necessarie nello sviluppo dei computer quantistici (bassissima temperatura e/o campi elettromagnetici particolarmente intensi per poter modificare gli stati degli atomi di idrogeno ad esempio) sono un altro impedimento per la massificazione di questa tecnologia come invece è successo con i computer classici che, potendo disporre di prezzi sempre più bassi e dimensioni ridotte, sono diventati uno strumento presente in ogni casa.
Facilmente il futuro dei computer quantistici sarà simile a quello che già IBM sta testando, ovvero il Cloud.
Mentre adesso si può accedere al computer IBM tramite Cloud solamente per provare a programmare, in futuro utilizzeremo algoritmi quantistici direttamente dal nostro smartphone per accedere ai servizi che necessitano di computer quantistici per essere eseguiti e che saranno ospitati su server remoti, trasformando il nostro dispositivo in un semplice terminale intelligente.
NOTE ALL’ARTICOLO: alcuni concetti sono stati semplificati allo scopo di renderli comprensibili dato che potevano essere difficili da capire; allo stesso modo sono tate utilizzate parole che non sono i termini esatti ma che aiutano a comprendere l’articolo ad un numero maggiore di utenti
